(Bonar Wahyu Hidayat / 21090115140140) Analisis varians (analysis of variance, ANOVA)

1. Pengertian Anova
 Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama lain, seperti analisis ragam, sidik ragam, dan analisis variansi. Ia merupakan pengembangan dari masalah Behrens-Fisher, sehingga uji-F juga dipakai dalam pengambilan keputusan. Analisis varians pertama kali diperkenalkan oleh Sir Ronald Fisher, bapak statistika modern. Dalam praktik, analisis varians dapat merupakan uji hipotesis (lebih sering dipakai) maupun pendugaan (estimation, khususnya di bidang genetika terapan). Berikut Hipotesis dalam anova :
H0: μ1 = μ2 = μ3 = ... = μn, Tidak ada perbedaan yang nyata antara rata-rata hitung dari n kelompok
H1: μ1 ≠ μ2 ≠ μ3 ≠ ... ≠ μn, Ada perbedaan yang nyata antara rata-rata hitung dari n kelompok

Uji hipotesis dengan ANOVA digunakan, setidaknya karena beberapa alasan berikut:

1.  Memudahkan analisa atas beberapa kelompok sampel yang berbeda dengan resiko kesalahan terkecil.

1.  Mengetahui signifikansi perbedaan rata-rata (μ) antara kelompok sampel yang satu dengan yang lain. Bisa jadi, meskipun secara numeris bedanya besar, namun berdasarkan analisa ANOVA, perbedaan tersebut TIDAK SIGNIFIKAN sehingga perbedaan μ bisa diabaikan. Sebaliknya, bisa jadi secara numeris bedanya kecil, namun berdasarkan analisa ANOVA, perbedaan tersebut SIGNIFIKAN, sehingga minimal ada satu μ yang berbeda dan perbedaan μ antar kelompok sampel tidak boleh diabaikan.

1.  Analisis varians relatif mudah dimodifikasi dan dapat dikembangkan untuk berbagai bentuk percobaan yang lebih rumit. Selain itu, analisis ini juga masih memiliki keterkaitan dengan analisis regresi. Akibatnya, penggunaannya sangat luas di berbagai bidang, mulai dari eksperimen laboratorium hingga eksperimen periklanan, psikologi, dan kemasyarakatan.

2. Jenis-jenis Anova

Sesuai dengan banyaknya faktor yang terlibat, maka anava dibedakan secara garis besar menjadi dua yaitu :

1)      Anava tunggal atau anova satu jalan

2)      Anava ganda atau anova lebih dari satu jalan.

-Analisis Variansi Satu Jalur-

 Yang dimaksud dengan analisis varians satu jalan adalah analisis varians yang digunakan untuk mengolah data yang hanya mengenal satu variable pembanding.

Dinamakan analisis varians satu arah, karena analisisnya menggunakan varians dan data hasil pengamatan merupakan pengaruh satu faktor.Dari tiap populasi secara independen kita ambil sebuah sampel acak, berukuran n₁ dari populasi kesatu, n₂ dari populasi kedua dan seterusnya berukuran n_k dari populasi ke k. Data sampel akan dinyatakan dengan Y_ij yang berarti data ke-j dalam sampel yang diambil dari populasi ke-i. ( Sudjana.1996.Metoda Statistika.Bandung:Tarsito Bandung).

ANAVA satu jalur yaitu analisis yang melibatkan hanya satu peubah bebas. Secara rinci, ANAVA satu jalur digunakan dalam suatu penelitian yang memiliki ciri-ciri berikut:1. Melibatkan hanya satu peubah bebas dengan dua kategori atau lebih yang dipilih dan ditentukan oleh peneliti secara tidak acak. Kategori yang dipilih disebut tidak acak karena peneliti tidak bermaksud menggeneralisasikan hasilnya ke kategori lain di luar yang diteliti pada peubah itu. Sebagai contoh, peubah jenis kelamin hanya terdiri atas dua ketgori (pria-wanita), atau peneliti hendak membandingkan keberhasilan antara Metode A, B, dan C dalam meningkatkan semangat belajar tanpa bermaksud menggeneralisasikan ke metode lain di luar ketiga metode tersebut.

1.             Perbedaan antara kategori atau tingkatan pada peubah bebas dapat bersifat kualitatif atau kuantitatif.

2.             Setiap subjek merupakan anggota dari hanya satu kelompok pada peubah bebas, dan dipilih secara acak dari populasi tertentu. (Furqon. 2009. Statistika Terapan untuk Penelitian. Cetakan ketujuh. ALFABETA: Bandung)

Tujuan dari uji anova satu jalur adalah untuk membandingkan lebih dari dua rata-rata. Sedangkan gunanya untuk menguji kemampuan generalisasi. Maksudnya dari signifikansi hasil penelitian. Jika terbukti berbeda berarti kedua sampel tersebut dapat digeneralisasikan (data sampel dianggap dapat mewakili populasi). Anova satu jalur dapat melihat perbandingan lebih dari dua kelompok data. (Riduwan.2008.Dasar-dasar Statistika.Bandung:Alfabeta)

Anova pengembangan atau penjabaran lebih lanjut dari uji-t .Uji-t atau uji-z hanya dapat melihat perbandingan dua kelompok data saja. Sedangkan anova satu jalur lebih dari dua kelompok data. Contoh: Perbedaan prestasi belajar statistika antara mahasiswa tugas belajar (X1), izin belajar (X2) dan umum (X3).

Anova lebih dikenal dengan uji-F (Fisher Test), sedangkan arti variasi atau varian itu asalnya dari pengertian konsep “Mean Square” atau kuadrat rerata (KR).

Rumusnya :

KR=JK/db

Dimana: JK = jumlah kuadrat (some of square)

                 db  = derajat bebas (degree of freedom)

-Analisis Variansi Dua Jalur-
Analisis varians dua jalan merupaka teknik analisis data penelitian dengan desain faktorial dua faktor. Dalam penelitian ini terdapat dua variable yang digunakan untuk dasar peninjauan sekor utntuk variable terikat. Anava dua jalan mempunyai judul kolom dan judul baris dengan menggunakan klasifikasi dua variable yang digunakan sebagai dasar tinjauan sekor untuk variable terikat. Anava dua jalan yang juga disebut dengan anava modal AB mempunyai dua variabel. Model diagram analisis dua jalan dapat berupa dua alternative.

Two way ANOVA digunakan untuk menguji hipotesis komparatif rata-rata k sampel bila peneliti melakukan kategorisasi terhadap sampel kedalam beberapa blok, sehingga bila variabilitas atau sumber keragaman pada uji One Way ANOVA berasal dari perlakuan dan galat, maka pada two way ANOVA sumber keragaman tidak hanya berasal dari perlakuan dan galat, tapi juga berasal dari blok.

Berikut adalah langkah-langkah dalam perhitungan ANOVA dua jalur (two way ANOVA):

a.   Identifikasi nilai: t (jumlah perlakuan), r (jumlah blog),

a.   hitung jumlah pengamatan total (n), yaitu: n = r x t,

a.   Hitung jumlah kuadrat total dengan rumus:

1. 

1. 
   
   

   Hitung jumlah kuadrat perlakuan dengan rumus: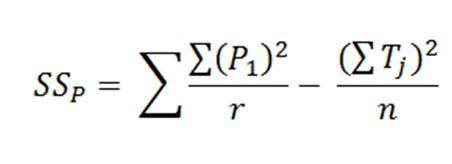
   

1. 
   
   

   Hitung jumlah kuadrat antar blok dengan rumus:
   

1. 
   
   

   Cari harga F-Hitung dengan menggunakan rumus yang tertera pada tabel.
   

g.  Cari harga F tabel dengan mempertimbangkan (1) tingkat signifikansi (α), (2) df1 yaitu df dari MS terbesar, dan (3) df2 yaitu df dari MS terkecil.

a.   Bandingkan harga F Hitung dengan F tabel.

(1) Bila F Hitung < F tabel, maka Ho diterima, yang berarti rata-rata kedua perlakuan tidak berbeda secara signifikan,

(2) Bila F Hitung > F tabel, maka Ho ditolak dan H1 diterima, yang berarti rata-rata kedua perlakuan berbeda secara signifikan.

Untuk lebih jelasnya, lihat contoh kasus berikut:
Seorang peneliti ingin mengetahui apakah ada pengaruh yang signifikan dari beberapa jenis pupuk (pupuk A, B, C, D, E dan F) terhadap pertumbuhan tanaman jagung di sebuah wilayah. Peneliti tersebut kemudian membagi petak percobaan kedalam 3 blok berdasarkan tingkat kesuburannya, yaitu: I= tingkat kesuburan rendah, 2= sedang, dan 3 = tinggi. Penelitian disusun berdasarkan desaian Rancangan Acak Kelompok, dan yang menjadi parameter adalah bobot tongkol jagung (g).

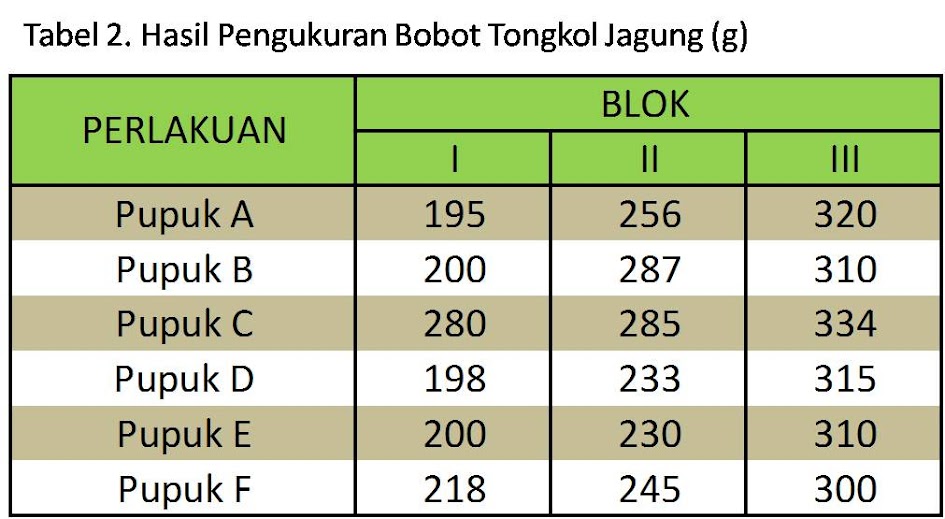
Setelah dilakukan pengukuran terhadap berat tongkol jagung, maka diperoleh hasil sebagai berikut:

Untuk mengetahui apakah ada perbedaan signifikan antar perlakuan, maka dilakukan uji ANOVA 2 arah (two way ANOVA). Proses pengerjaannya dapat dilakukan secara cepat dan mudah dengan menggunakan aplikasi program Microsoft Excel.

Two Way Anova

Two Way Anova disebut juga dengan Anova 2 Arah atau Analisis Varian 2 Faktor. ANOVA dua arah membandingkan perbedaan rata-rata antara kelompok yang telah dibagi pada dua variabel independen (disebut faktor). Anda perlu memiliki dua variabel independen berskala data kategorik dan satu variabel terikat berskala data kuantitatif/numerik (interval atau rasio).

Pengertian Anova

Anova merupakan singkatan dari “analysis of varian” adalah salah satu uji komparatif yang digunakan untuk menguji perbedaan mean (rata-rata) data lebih dari dua kelompok. Ada dua jenis Anova, yaitu analisis varian satu faktor (one way anova) dan analisis varian dua faktor (two ways anova). Pada artikel ini hanya akan dibahas analisis varian dua faktor.

Asumsi ANOVA

Untuk melakukan uji Anova, harus dipenuhi beberapa asumsi, yaitu:

1. Sampel berasal dari kelompok yang independen

1. Varian antar kelompok harus homogen

1. Nilai Residual berdistribusi normal (Pelajari juga tentang uji normalitas)

Untuk lebih jelasnya tentang ANOVA, anda pelajari artikel kami yang berjudul “One Way Anova dalam SPSS“.

Tutorial Two Way Anova dalam SPSS

Berikut akan kami jelaskan tutorial Two Way Anova dalam SPSS.

Kita ambil contoh penelitian yang berjudul “Pengaruh Gender dan Pendidikan Terhadap Nilai Ujian Fisika”.

Agar lebih mudah, sebaiknya anda download contoh file SPSS (.sav) yang akan digunakan dalam uji coba ini di link berikut:
Two Way Anova.sav

Langkah pertama adalah siapkan dulu data sebagai berikut:

Two Way Anova Dataset Excel

Buka Aplikasi SPSS For Windows:

• Buka Tab Variable View: Buat 3 variabel dengan ketentuan sebagai berikut:

• Variabel independen: 1. “Gender” dengan kategori Pria dan Wanita. Measure Nominal, Decimals=0, Type Numeric dan isi value: 1= Pria, 2=Wanita.

• Variabel independen: 2. “Pendidikan” dengan kategori SLTP, SLTA dan PT. Measure Nominal, Decimals=0, Type Numeric dan isi value: 1= SLTP, 2=SLTA, 3=PT.

• Variabel dependen: “Ujian”, Decimals=0, Measure Scale, Type Numeric.

Dataview

Buka Tab Data View: Isi data seperti di bawah ini:

Two Way Anova Dataset

• Setelah data terisi, pada menu, Klik Analyze, General Linear Model, Univariate. Maka akan mucul jendela sbb: Masukkan Ujian ke kotak Dependent Variable, masukkan Gender dan Pendidikan ke kotak Fixed factor(s). (Kotak Random factor (s) dan Covariate(s) tidak akan kita gunakan dalam Two Ways Anova, kotak tersebut akan digunakan pada “Uji Ancova“).

SPSS Proses

• Klik Plot, maka akan muncul jendela seperti di bawah ini: Masukkan Gender  ke kotak Horizontal Axis dan Pendidikan ke kotak Separate Lines.

SPSS Plot

• Klik Add, maka akan tampak sbb:

SPSS Plot Continue

• Klik Continue.

• Klik Post Hoc, maka muncul jendela sbb: Masukkan Pendidikan ke kotak Post Hoc Test for. Centang Tukey

Two Way Anova SPSS Post Hoc

• Klik Continue

• Klik Options, maka akan muncul jendela sbb: Masukkan Gender, Pendidikan, dan Gender*Pendidikan ke dalam kotak Display Means for. Pada Display centang Descriptive statistics dan Homogentity test.

Two Way Anova SPSS Homogenity

• Klik Continue

• Klik OK

• Lihat Hasil!

Artikel ini hanya menjelaskan langkah demi langkah melakukan uji two way anova, sedangkan membaca output dan interprestasinya akan dijelaskan dalam artikel berikutnya yang berjudul: “Interprestasi Output Two Way Anova Dalam SPSS“.

Terima Kasih.